خصائص معادلات السوائل
جدول المحتويات
اللزوجة النموذجية
على عكس الضغط الهيدروستاتيكي ، لا يتم ممارسة قوة القص بشكل عمودي على السطح البيني لجزيئي المائعين ، ولكن بشكل عرضي. تبنى Barré de Saint-Venant بعد ذلك الفرضية القائلة بأن قوى القص تظهر في اتجاه التدفق – بشكل أكثر دقة في اتجاه الحركة النسبية للجسيمين المائعين – وأنها متناسبة مع السرعة النسبية للجسيمين.
يتضح أن نتيجة قوى القص هذه ، والتي تعارض السرعة النسبية لجسيمين مائعين على اتصال ، هي اللزوجة التي تسهل الفروق في السرعة بين نقطة من السائل وجيرانها. ثم تتوافق قوة اللزوجة ، في معادلات نافييه-ستوكس ، مع معامل اللزوجة ، المشار إليه بالحرف اليوناني n ، مضروبًا في مجموع المشتقات المكانية من الدرجة الثانية للسرعة
خصائص معادلات السوائل : خطوة مهمة إلى الأمام في إنشاء معادلات
وهكذا ، اتخذ Barré de Saint-Venant خطوة مهمة إلى الأمام في إنشاء معادلات Navier-Stokes. ومع ذلك ، لا يرتبط اسمه بهم. لماذا ؟ في الواقع ، لم تُطبع أعمال Barre de Saint-Venant ، وبالتالي لم تُنشر إلا في عام 1843. بشكل مستقل ، نشر الفيزيائي البريطاني جورج غابرييل ستوكس في عام 1845 نتائج مماثلة في أطروحته حول نظريات الاحتكاك الداخلي للسوائل المتحركة . بشكل غير عادل إلى حد ما ، من بين الاسمين ، ظهر اسم ستوكس فقط ، بالإضافة إلى اسم نافيير ، لتعيين معادلات حركة المائع.
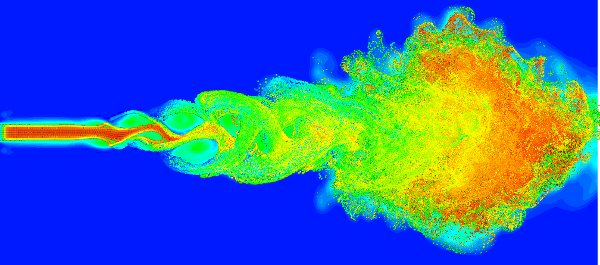
إقرأ أيضا:5 نصائح سريعة لتحسين قوتك الشرائيةلنعد إلى الصعوبات المرتبطة بمعادلات نافييه-ستوكس. أحد الشواغل الرئيسية هو الاضطراب ، والذي غالبًا ما يظهر في التدفقات السريعة. يمكن رؤية الطبيعة الرائعة والمثيرة للاهتمام لهذه الظاهرة من تجربة بسيطة للغاية. يكفي ملاحظة التدفق البطيء للماء في أنبوب زجاجي أفقي يضاف إليه قطرة ملونة: يمتد القطرة إلى خيط يبدأ بعد مسافة معينة بالدوران وبالتالي يختلط مع الماء بشكل عشوائي. أصبح التيار مضطربًا بشكل عفوي!
مشكلة شائكة: اضطراب
الاضطراب هو ظاهرة اهتم بها علماء الفيزياء والرياضيات لفترة طويلة ، دون أن ينجحوا في اقتراح تفسير ووصف مرضيين لها. هذا لا يمنع استغلالها من قبل المهندسين. نعلم على سبيل المثال أن الاستيقاظ المضطرب خلف جسم متحرك يسبب مقاومة ، أو قوة سحب ، أقل أهمية من اليقظة الصفائحية (غير المضطربة). هذا هو السبب في أن ملف تعريف خوذات الدراجات النارية الحديثة له فترات استراحة ، مما يؤدي إلى اضطراب تدفق الهواء في اتجاه مجرى الخوذة.
خصائص معادلات السوائل : الاضطراب هو ظاهرة تنطوي على مقاييس أطوال متعددة
الاضطراب هو ظاهرة تنطوي على مقاييس أطوال متعددة ، والتي ترتفع إلى المقياس المجهري. ومع ذلك ، في هذا المقياس ، يفقد وصف المائع على أنه وسيط مستمر ، وهو أساس معادلات نافيير-ستوكس ، أهميته. علاوة على ذلك ، فإن الطرق العددية لحل هذه المعادلات تتم عن طريق التقدير ، وهو تقسيم الفضاء إلى أحجام صغيرة حيث يُفترض أن يكون التدفق منتظمًا – وهذا ليس تقريبًا جيدًا إذا كان التدفق مضطربًا حتى مقاييس أصغر من تلك الموجودة في تقديرية.
إقرأ أيضا:مرجان العمقلذلك ليس من المؤكد على الإطلاق ، في الأنظمة المضطربة ، أن الدقة العددية لمعادلات نافيير-ستوكس توفر حلولًا تشبه إلى حد كبير السلوك الحقيقي للسائل. في الواقع ، في المحاكاة العددية ، نعتمد على ما نسميه نماذج الاضطراب ، حيث نقدم بطريقة ظاهرية مخصصة ، معلمات من المفترض أن تتضمن تفاصيل الاضطراب التي يتعذر الوصول إليها. تؤدي هذه النماذج ، التي توجد بها عائلات كاملة ، إلى نتائج مفيدة أكثر أو أقل اعتمادًا على مجالات التطبيق. لكنها ليست سوى حل مؤقت بدون فهم حقيقي للاضطرابات.
يجب التأكيد أيضًا على أن الخوارزميات العددية لا تحل بالفعل معادلات نافييه-ستوكس: فهي تهدف إلى تقريب حلول هذه المعادلات ، بافتراض وجودها. على سبيل المثال ، يحل التقديري محل المشتقات ، المحددة رياضيًا بواسطة ممر إلى الحد الأقصى ، بحواجز بسيطة للاختلافات. بمعنى آخر ، نستبدل السؤال المطروح بسؤال آخر أبسط والذي يقترب من السؤال الأصلي قدر الإمكان ، بينما نأمل أن يكون حل هذه المشكلة الجديدة قريبًا جدًا من حل السؤال الأولي. ومع ذلك ، يجب إثبات ذلك على أساس كل حالة على حدة.
هل يعكس النموذج الواقع؟
غالبًا ما يُعتقد أن إجراء تحقق موثوق به هو مقارنة الحلول العددية بالبيانات التجريبية. لكن هذه فكرة خاطئة. يمكننا بالطبع تعديل نموذج الاضطراب تدريجيًا حتى يقترب الحل العددي من البيانات التجريبية بدقة كبيرة ، ولكن هذه ليست الطريقة التي نحسن بها فهمنا للاضطراب.
إقرأ أيضا:رابطة الدول والأقاليم فيما وراء البحارعلاوة على ذلك ، كما أشرت إليه ، فإن معادلات نافييه-ستوكس تشكل فقط نموذجًا رياضيًا لتدفق مائع لزج ، وليس من المضمون أن يتوافق هذا النموذج دائمًا مع الواقع المادي.
في المقام الأول ، تشير حقيقة التعامل مع دالة قابلة للتفاضل v (r ، t) إلى وجود وسيط موحد حيث يمكن للمرء في كل نقطة وفي أي لحظة ربط السرعة. ومع ذلك ، فإن الموقف الذي يتماشى أكثر مع الواقع هو الموقف الذي يتحرك فيه عدد كبير من الجزيئات بطريقة غير منظمة ، ويتبادل الزخم والطاقة فيما بينها. بالمعنى الدقيق للكلمة ، يمثل الحجم v (r ، t) في الواقع متوسطًا لجميع الجزيئات الموجودة في حجم صغير يحيط بالنقطة r.
خصائص معادلات السوائل : من الممكن الاعتماد على وصف الطبيعة المجهرية للوصول إلى معادلات نافييه-ستوكس
في الواقع ، من الممكن الاعتماد على وصف الطبيعة المجهرية للوصول إلى معادلات نافييه-ستوكس ، مع بعض التقريبات. يمكننا بشكل خاص الاعتماد على النظرية الحركية للغازات ، التي طورها الفيزيائي النمساوي لودفيج بولتزمان (1844-1906) ، والتي تقدم وصفًا احتماليًا وإحصائيًا لما يحدث على المستوى الجزيئي. لكن المرور من المقياس الجزيئي إلى الوسائل المحددة في أي نقطة أمر دقيق ، وليس من المؤكد أن لزوجة مائع آخر غير الغاز المثالي موصوفة بشكل صحيح من خلال المصطلح المقابل في معادلات نافيير. ربما نحتاج إلى تجاوز المشتقات من الدرجة الثانية وتضمين المشتقات ذات الرتبة الأعلى لنمذجة أكثر دقة؟
قبل بضع سنوات ، اقترح عالم الرياضيات التشيكي Jindrˇich Necˇas (1929-2002) نموذجًا بديلًا للزوجة على أمل إثبات وجود حلول للمعادلات المعدلة بهذه الطريقة. ومع ذلك ، لم تنجح ، وما زالت معادلات نافييه-ستوكس تمثل أفضل نمذجة متاحة لنا.
نظرًا لأن بيان وجود الحلول وتفردها يبدو بعيد المنال في الوقت الحالي ، يركز علماء الرياضيات على الأهداف الوسيطة. على سبيل المثال ، هل هناك حل غير مادي واضح لمعادلات نافييه-ستوكس؟ إذا كان الأمر كذلك ، فسيكون من الواضح أن هذه المعادلات لا تشكل وصفًا مناسبًا للواقع. على العكس من ذلك ، إذا نجحنا في استبعاد ظهور بعض الحلول غير المادية ، فسنقترب قليلاً من الدليل المطلوب.
سيكون الحل غير المادي ، على سبيل المثال ، حلاً تزداد فيه الطاقات الحركية والمحتملة للنظام. في الواقع ، بما أن الاحتكاك يبدد الطاقة الحركية في الحرارة ، يجب أن يظل مجموع الطاقة الحركية والطاقة الكامنة أقل ، أو على الأكثر مساوية لقيمته الأولية. من السهل نسبيًا إثبات أن هذا هو الحال بالنسبة إلى معادلات نافييه-ستوكس.
حلول تتفجر …
هناك حالة أخرى غير مادية تتوافق مع تركيز طاقة النظام بالقرب من نقطة واحدة ، وبالتالي تميل كثافة الطاقة نحو اللانهاية في هذه المرحلة. يطلق المتخصصون على هذه الحالة اسم التفجير.
لفهم هذه المشكلة بشكل أفضل ، دعنا نجري التجربة الفكرية التالية: باستخدام ملعقة كبيرة ، نطبق حركة دوارة على الماء الذي يملأ به دلو. بمجرد بدء الدوران ، نحدد في لحظة معينة التدفق الدوار الذي تم الحصول عليه على أنه الشروط الأولية لمعادلات Navier-Stokes. في أي نقطة في الجرافة ، هل يمكن أن تزداد سرعة السائل بلا حدود وبالتالي تؤدي إلى انفجار؟ مثل هذا السلوك ، بالطبع ، لم يلاحظ أبدًا. ولكن هل يوجد لكل ذلك ، في المعادلات ، خاصية تمنع حدوث مثل هذا التفجير؟
يعرف علماء الرياضيات في الواقع معادلات تفاضلية غير خطية أخرى تقدم ظواهر انفجار غير فيزيائية. هذا هو الحال أيضًا مع معادلات أويلر: على سبيل المثال ، هناك حلول تتوافق مع التطور المتفجر للسائل ، بينما يكون الأخير ثابتًا في البداية في كل مكان!
خصائص معادلات السوائل : باستثناء حالات قليلة نادرة للغاية
باستثناء حالات قليلة نادرة للغاية ، لا يمكن إيجاد حلول رياضية واضحة (أي غير رقمية) لمعادلات نافيير-ستوكس. أيضًا ، للبحث عن حلول أو لتوصيفها حتى بدون العثور عليها ، يتعين على علماء الرياضيات اللجوء إلى طرق غير مباشرة.
على سبيل المثال ، يعتبرون أن الحل المسبق للمعادلات هو وظيفة معينة تنتمي إلى مساحة وظيفية مناسبة ، أي مساحة مجردة ذات بُعد غير محدود بشكل عام ، تكون نقاطها وظائف ليس لها خصائص مقيدة للغاية. من خلال التحرك المستمر في هذا الفضاء ، نتحرك باستمرار من وظيفة إلى أخرى. وحتى نتمكن من مقارنة الوظائف والنظر في تسلسل الوظائف ، يجب أن يكون الفضاء الوظيفي مزودًا بمفهوم المسافة والحد.
في البداية ، اختار علماء الرياضيات المساحات الوظيفية التي. تكون عناصرها وظائف منتظمة بدرجة كافية (مما يعني على سبيل المثال وظائف قابلة للتفاضل عدة مرات). لكن تبين أن هذا لم يكن كافياً وكان. من الضروري أن يضع المرء نفسه في مساحات أكبر ، تحتوي أيضًا على وظائف متقطعة أو غير قابلة للتفاضل.
من خلال عدم اعتبار هذه الوظائف بالمعنى الدقيق للكلمة . ولكن تكاملات منتجها مع “وظيفة الاختبار” (وظيفة عشوائية جزئيًا ، ولكن لها خصائص مثل أن يكون التكامل المدروس دائمًا له قيمة محددة جيدًا) ، فإننا نصل .إلى فكرة “الحل الضعيف” لمعادلات نافييه-ستوكس ، مجموعة الحلول الضعيفة بما في ذلك الحلول العادية.
في عامي 1933 و 1934
في عامي 1933 و 1934 ، تمكن عالم الرياضيات الفرنسي جان ليراي من إثبات وجود مثل هذه الحلول الضعيفة. لقد أظهر أيضًا وجود الحلول المنتظمة وتفردها ، ولكن فقط لأوقات محدودة ، أي دون أن يكون قادرًا على ضمان .ألا تصبح هذه الحلول فريدة بعد وقت طويل بما فيه الكفاية.
بعد ثلاثين عامًا ، في عام 1964 ، قام اليابانيان هيروشي فوجيتا وتوسيو كاتو بتمديد. نتيجة ليراي بطريقة أكثر قوة ، والتي تبناها العديد من علماء الرياضيات. وهكذا أثبت الباحثان وجود وتميز الحلول. المنتظمة على مستوى العالم في الوقت المناسب ، ولكن بالنسبة للبيانات الصغيرة (السوائل قريبة من عدم الحركة).
تم الحصول على نتيجة مهمة أخرى باستخدام طريقة مشابهة لتلك التي استخدمها H. هي حلول منتظمة على مستوى العالم في الوقت المناسب ، لبيانات متذبذبة بشدة.
في الآونة الأخيرة ، في حوالي عام 2010 ، قدم جان إيف شيمن ، من جامعة بيير وماري كوري ، وإيزابيل غالاغر ، من جامعة باريس ديدرو ، فئات بيانات ، ليست بالضرورة صغيرة ولا متذبذبة .بالضرورة ، والتي لها معادلات نافييه-ستوكس حل منتظم عالمي ، في كل الفضاء.
خصائص معادلات السوائل : على الرغم من التقدم ، فإن المشكلة تقاوم
على الرغم من هذه التطورات وغيرها ، ليس لدينا بعد بيان عام عن وجود الحلول المنتظمة وتفردها. لقد فشلت المحاولات حتى الآن ، لأنه عند محاولة الانتقال من الحلول الضعيفة إلى الحلول. العادية ، تظهر شذوذ ، مثل تلك المذكورة عن دلو الماء.
لذلك ركزت بعض الدراسات على تقييم مقدار النقاط التي يمكن أن تتطور فيها التفردات. في عام 1982 ، أظهر الأرجنتيني لويس كافاريلي ، والأمريكي روبرت كون والكندي لويس نيرنبرغ أن .مجموعة هذه النقاط هي في .أقصى حد من الصفر (وهذا يعني أنه من المحتمل أن يكون هناك عدد لا نهائي منها ، لكنها أكثر ندرة من مجموعة النقاط. النقاط التي يكون الحل فيها منتظمًا).
تم تحسين هذه النتيجة بشكل ملحوظ في حوالي عام 2003 من قبل الإسباني. لويس إسكوريا والروس غريغوري سيريجين وفلاديمير سفيراك ، الذين درسوا الانتظام المحلي لحلول ليراي الضعيفة ووضعوا معيارًا يجعل من الممكن التأكيد على أن الحل يؤدي إلى انفجار.
للتلخيص ، هناك حلان ممكنان للمشكلة التي اقترحها معهد كلاي. إما أن نظهر أنه .في ظل الافتراضات الواقعية ، يوجد حل منتظم لمعادلات نافيير-ستوكس لجميع الأوقات . أو ، على العكس من ذلك ، تظهر التفردات بشكل عام. على أي حال ، ستمثل النتيجة تقدمًا كبيرًا في دراسة هذه المعادلات التفاضلية الجزئية.